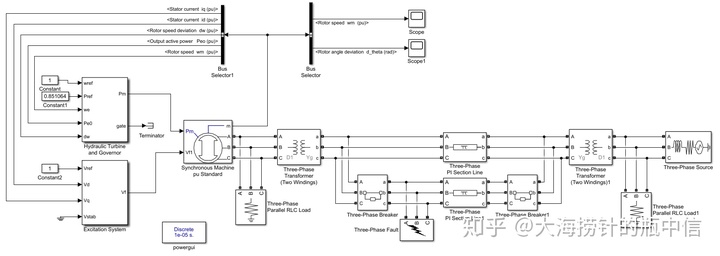
《MATLAB/Simulink电力系统建模与仿真》第2版p125
简单系统,短路故障(II段)发电机摇摆曲线δ-t(转子运动方程——两个一阶非线性常微分方程):
已知切除故障时间(III段),求δ-t曲线判断系统稳定性
教材常用分段计算法和常微分方程数值解法——改进欧拉法,但是由于MATLAB进行常微分方程求解算法中没有改进欧拉法,编程时采用Runge-Kutta龙格-库塔法。
%****发电机转子摇摆曲线的非线性一阶微分方程的Runge-Kutta龙格-库塔法的m函数***
%**************************************************************************
function Yd=power_tra(t,YY)
%t是标量形式的自变量
%YY是列向量
global y0 Tj Pt E U X1 %在函数中定义全局变量传递参数
%发电机转子摇摆曲线的微分方程
Yd=[(YY(2)-1)*y0;(Pt-(E*U/X1)*sin(YY(1)))/Tj];求解微分方程程序
%求解发电机转子摇摆曲线的微分方程
%故障发生后的摆动曲线(没有切除故障)
%在主程序中定义全局变量传递函数
global y0 Tj Pt E U X1
y0=2*pi*50; Tj=11.28; Pt=1; E=1.47; U=1;
%系统转移电抗
X1=2.82; %故障时
%指定解算微分方程的时间区间
tspan=[0.0 0.3];
%给定初始向量
y1=[31.54*pi/180;1]; %故障时
%求解微分方程
[t,YY]=ode45('chapter6_1_transient_stability_Runge_Kutta',tspan,y1);
%ode45是一种变步长的采用Runge-Kutta的Nonstiff(非刚性)常微分方程算法(很重要)
%输出求解结果结果
x=YY(:,1);
y=YY(:,2);
%绘制曲线
subplot(2,1,1) %功率角δ曲线
plot(t,x*180/pi);
ylabel('delta/deg');
grid on
subplot(2,1,2) %转子转速ω曲线
plot(t,y*100*pi);
xlabel('t/s');
ylabel('omega/(rad/s)');
grid on建立simulink仿真模型: